Eassy on Nuclear Stability page4

n =
p-2	p-1	p	p+1	p+2
	H 1		n
		H 2
	He 3		H 3
		He 4











		O 16

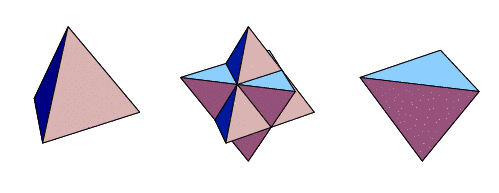
Dodecahedron

After looking at both the Tetrahedron and the Dodecahedron can you predict how the two could be made to coinside.

We now have on our table more than the two stable isotopes of both Hydrogen and Helium; two Lithium, one Beryllium, two Boron, two Carbon, two for Nitrogen and Oxygen-16, the most common isotope of Oxygen

This makes a total of 14 nuclides, 15 if you would count the neutron. Can you place them on the chart at left.

Impart no quality or characteristic to nucleons other than a space filling property and yet not asigning them any sort of hard ball nature. Perhaps with ease you may intuit why nuclides of isobars of 1, 4, and 16 would be stable and more so durable and abundent.

n =
p-2	p-1	p	p+1	p+2
	H 1
		H 2
	He 3
		He 4

		Li 6
			Li 7

			Be 9
		B 10
			B 11
		C 12
			C 13
		N 14
			N 15
		O 16

We observe He-4 and O-16 are in the same column and may well deduce that protons and neutrons like to be paired up. Execpt in the case of H-2 where the single proton alone is favored.

The next thing we readly see that each isobar 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 14, 15 and 16 have a single stable speices. There is a relationship between the proton and neutron in the isobar 1.
We also see nature favors no isobar-5 and isobar-8. If we can find reasons why this is so then we should look back again at each of the other stable isobars that we might discern why nature favors their stability if not abundence as is the case of 1, 4, and 16.

The missing isobar-5, at first glance, appears to simply be a case of odd man out. That is for any arangement of five nucleons the tendancy to distribute mass evenly results in excluding one from that pattern of distribution.

All Isobars to six
		H-1
			H-2
		He-3		H-3
	Li-4		He-4		H-4
		Li-5		He-5
	Be-6		Li-6		He-6

The odd man out situation of isobar-5 is remedied in isobar-6. Six is a Platonic number, that is one of the Platonic solids has six points(vertisies), and equaly divides a sphere.

The Octahedron

Taken together both isotopes of Lithium, which is not a very plentiful element, we see something interesting. Li-7 is very much more abundent than Li-6. Nature favors the isobar with the additional nucleon nested within!

With isobar-8 we have a distinct condition. Consider stacking four balls upon four more in the shape of a cube. The cube is a Platonic solid and distributes equaly within the sphere, should be stable! Perhaps the the tendancy to equaly distribute brings the nucleons out of a close packing arangement into a rolly-polly state. Examine the floppy condition of a house built without cross beams. It may be the case that nature so favors the Alpha particle that the isobar-8 readily disassociates into two helium atoms.

If one wanted to compare the binding energy of each of the nucides of the isobar-8 row, unstable as they are, it good that that be in a row. This was my impulse for developing the Incremental Table, a new type of table to portray any data pertinent.